Research Interests

Nano and micro mechanics

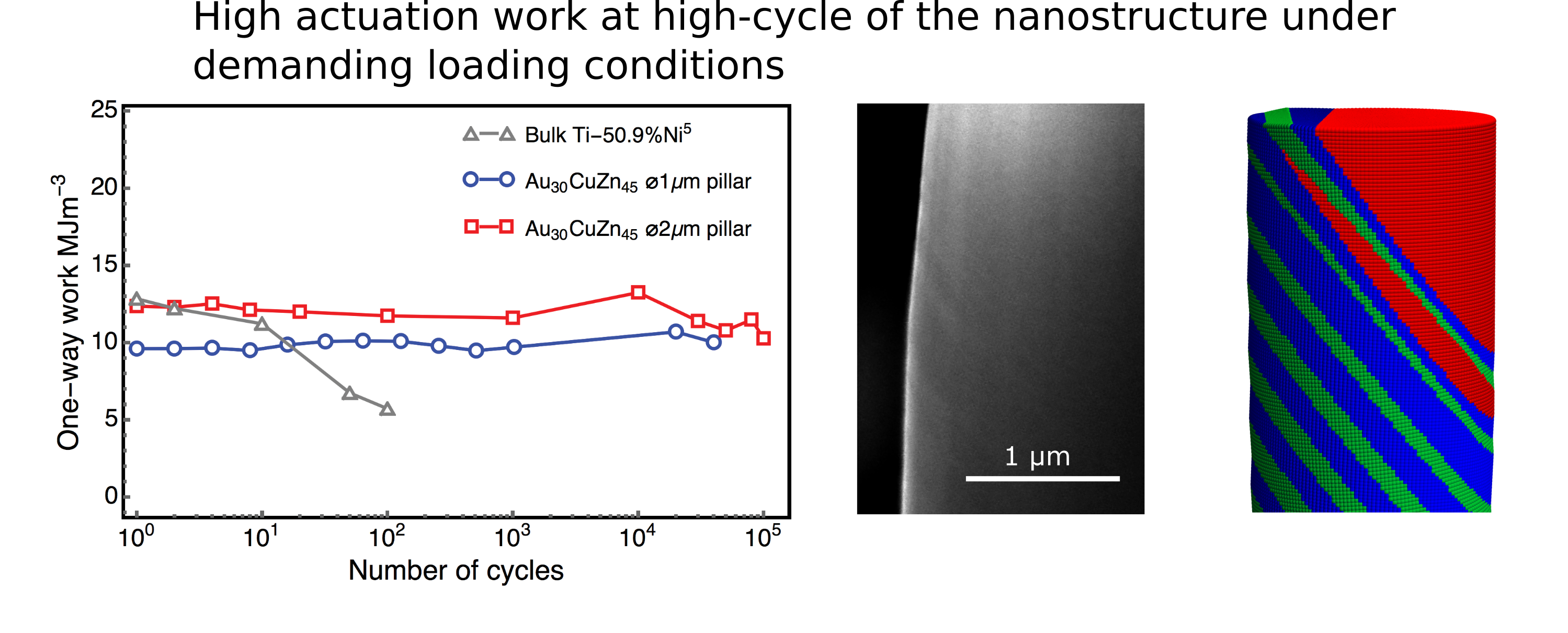
Shape memory alloys that produce and recover from large deformation driven by martensitic transformation are widely exploited in biomedical devices and microactuators. Generally their actuation work degrades significantly within first a few cycles and is reduced at smaller dimensions. Further, alloys exhibiting unprecedented reversibility have relatively small superelastic strain, 0.7%. These raise the questions of whether high reversibility is necessarily accompanied by small work and strain and whether high work and strain is necessarily diminished at small scale. Here we conclusively demonstrate that these are not true by showing that the pillars exhibit 12 MJ m−3 work and 3.5% superelastic strain even after 100,000 phase transformation cycles. Our findings confirm that the lattice compatibility dominates the mechanical behavior of phase-changing materials at nano to micron scales and points a way for smart microactuators design having the mutual benefits of high actuation work and long lifetime.

Low-hysteresis materials

Materials undergoing martensitic transformations have emerging applications in medical industry such as stents and orthodontic arch wires, known as shape memory alloys (SMAs). Recent years, these materials have been increasingly exploited for many new applications in microelectronics and energy conversion devices when the change of lattice parameters is linked to the sensitivity of multiferroic properties. A major problem with these materials is the loss of functionality upon phase transformation by which the thermal hysteresis is accumulated and increases, and the mechanical properties degrade upon cycling loading.

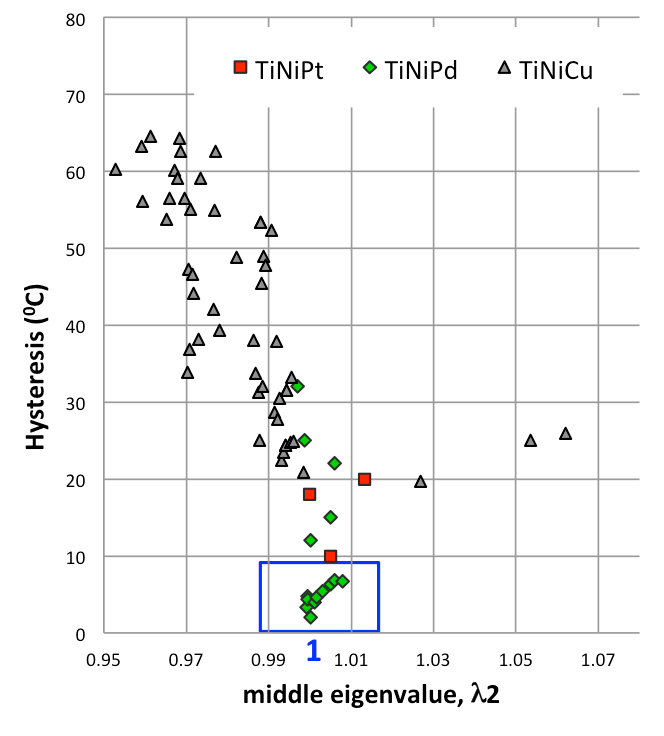
The origin of such degradation comes from the formation of microstructure consisting stressed-transition layers due to lattice mismatch at heterophase boundaries. It has been proven that when the lattice parameters satisfy a set of kinematic conditions of compatibility, both hysteresis and reversibility can be optimized, thus long life-time is achieved for these applications. One of the most important condition of compatibility is $\lambda_2 = 1$ where $\lambda_2$ denotes the middle eigenvalue of the transformation stretch tensor. The plot below shows that the thermal hysteresis in NiTi families of shape memory alloys is minimized at $\lambda_2 = 1$. Accordingly, the twinned martensite microstructure becomes twinless and the elastic transition layer between austenite and martensite is eliminated.

Cofactor Conditions

The Cofactor Conditions (CC) are the conditions of compatibility for the interface between the austenite and twinned martensite phases. For the type I and type II twin systems, beyond the condition that $\lambda_2 = 1$, the CC require that one of the 2-fold axes of austenite is unstretchable when the material undergoes phase transformation back and forth. For the compound twin system of martensite, it requires that both twinning plane normal and relative twin shear are perpendicular to the middle eigenvector of transformation stretch tensor, together with a mild inequality condition.

The mathematical forms of the Cofactor Conditions:

  • $\lambda_2 =1$ where $\lambda_2$ is the middle eigenvalue of $\mathbf U$.
  • $\Vert\mathbf U^{-1} \mathbf e\Vert = 1$ for type I twin, $\Vert\mathbf U \mathbf e\Vert = 1$ for type II twin, where $\mathbf e$ is one of the 2-fold axes of austenite.
  • $\mathbf e \cdot \mathbf v_2 = 0$, $\mathbf e^\perp \cdot \mathbf v_2 = 0$ and $(2\sqrt{1-(\mathbf e \cdot \mathbf v_1)^2(\mathbf e \cdot \mathbf v_3)^2}+1)\det \mathbf U^2 \geq 2$ for the compound twin. The vectors $\mathbf v_1$, $\mathbf v_2$ and $\mathbf v_3$ are three eigenvectors corresponding to the ordered eigenvalues of the transformation stretch tensor $\mathbf U$.

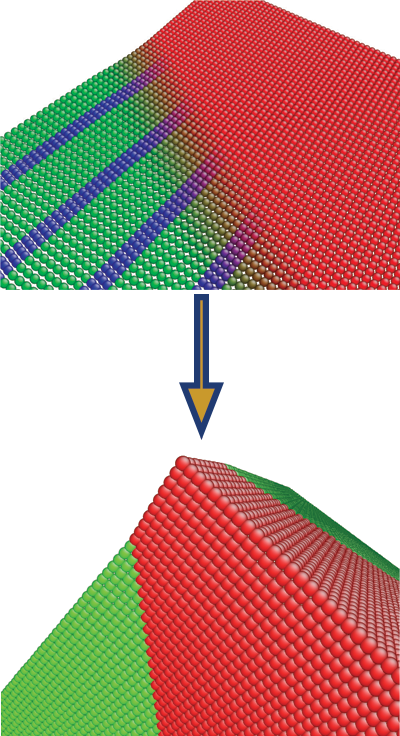
    • When the lattice parameters are tuned to satisfy the Cofactor Conditions for specific twin systems, great many configurations between the austenite and martensite variants can form to minimize the total free energy during the phase transformation. Therefore rich microstructures can be observed.

    Unusual microstructure of martensites for the Zn-Au-Cu shape memory alloy satisfying the cofactor conditions. HD video from Nature

    Algorithms and advanced structure characterization

    Determination of the stretch tensor between two crystalline phases are essential for both micro- and macro- scopic mechanical behaviours of materials undergoing structural transformation. In principle, such a stretch tensor is calculated based on the weak Cauchy-Born rule, i.e. there exists a linear transformation $\mathbf F$ mapping three linear independent lattice vectors of one phase, $\mathbf a_i$, to the primitive lattice vectors of the other phase, $\mathbf m_i$, such that $\mathbf F \mathbf a_i = \mathbf m_i$

    The lattice vectors $\mathbf a_i$ could underlie a sublattice of the original lattice of initial phase. The correspondence $\mathbf a_i \to \mathbf m_i$ giving least transformation strain $\Vert\mathbf F^T \mathbf F - \mathbf I\Vert$ is called the lattice correspondence for such structural transformation. We have implemented an algorithm StrucTrans to calculate the lattice correspondence and the associated transformation stretch tensor.

    To directly and quantitatively characterize the phase transformation, particularly the highly reversible martensite phase transformation showing large transformation strain, we have established a special apparatus for the Beamline 12.3.2 X-ray Laue Microdiffraction, Advanced Light Source, Lawrence Berkeley National Lab. It can be mounted to the synchrotron facility and provide an abrupt temperature gradient within a narrow gap across which the specimen is set.

    This experiment has been exploited for in-situ measurement of the orientation matrices for the austenite and martensite phases of the alloy Cu25Au30Zn45, which shows unusual austenite/martensite interfaces.

    Diffusional phase transformation

    For diffusional phase transformations that are almost irreversible but can be used for the synthesis of functional materials. Most of the functional composites are made by this method because the nanoscale inclusions are easily produced by the annealing process. The precipitates spread out the matrix are with the interesting applicable function. Thermoelectrics, luminescent materials, solid state fuel cells etc. are the successful applications.

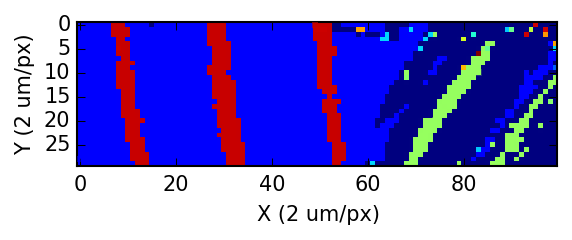
    Investigation of microstructures for the precipitates becomes very important because the orientations, shapes and volume fraction dominate the overall properties of the composites. All these control parameters are 3-dimensional quantities that can by visualized by the latest slice-and-view technique shown on the right. The colored chunks are precipitates seemed to be randomly distributed in whole matrix box. In fact, their orientation is predictable by a weak compatibility condition proposed in our recent paper (see publications) that predicts the elongated direction of the precipitates in the box lying on the crystallographically equivalent cones.

    The longest directions of the precipitates are those red lines shown in the statistical results. They are governed by four crystallographically equivalent cones determined by the weak compatibility condition. Moreover, the half-cone angles distribution is shown on the right that is fitted by a Gaussian distribution with standard deviation 5.60.